Cryptography and Network Security Basic Concepts
INTRODUCTION
Computer data often travels from
one computer to another, leaving the safety of its protected physical surroundings.
Once the data is out of hand, people with bad intention could modify or forge
your data, either for amusement or for their own benefit. Cryptography can
reformat and transform our data, making it safer on its trip between computers.
The technology is based on the essentials of secret codes, augmented by modern mathematics
that protects our data in powerful ways.
• Computer Security -
generic name for the collection of tools designed to protect data and to thwart
hackers
• Network Security - measures
to protect data during their transmission
• Internet Security -
measures to protect data during their transmission over a collection of interconnected
networks
Basic Concepts
Cryptography The
art or science encompassing the principles and methods of transforming an
intelligible message into one that is unintelligible, and then retransforming
that message back to its original form
Plaintext The
original intelligible message
Cipher text The
transformed message
Cipher An
algorithm for transforming an intelligible message into one that is
unintelligible by transposition and/or substitution methods
Key Some critical
information used by the cipher, known only to the sender& receiver
Encipher (encode) The
process of converting plaintext to cipher text using a cipher and a key
Decipher (decode) the
process of converting cipher text back into plaintext using a cipher and a key
Cryptanalysis The
study of principles and methods of transforming an unintelligible message back
into an intelligible message without knowledge of the key. Also called code
breaking
Cryptology Both
cryptography and cryptanalysis
Code An algorithm for
transforming an intelligible message into an unintelligible one using a
code-book
Cryptography
Cryptographic systems are generally classified along
3 independent dimensions:
Type of operations used for transforming
plain text to cipher text
All the encryption algorithms are based on two
general principles: substitution, in which each element in the plaintext
is mapped into another element, and transposition, in whichelements in
the plaintext are rearranged.
The number of keys used
If the sender and receiver uses same key then it is
said to be symmetric key (or)single key (or) conventional encryption.
If the sender and receiver use different keys then
it is said to be public key encryption.
The way in which the plain text is
processed
A block cipher processes the input and block
of elements at a time, producing output block for each input block.
A stream cipher processes the input elements
continuously, producing output element one at a time, as it goes along.
Basic Principles Security Goals:
The primary goal of network security are
Confidentiality, Integrity, and Availability. These three pillars of Network
Security are often represented as CIA
triangle.
·
Confidentiality − The function of
confidentiality is to protect precious business data from unauthorized persons.
Confidentiality part of network security makes sure that the data is available
only to the intended and authorized persons.
·
Integrity − This goal means maintaining
and assuring the accuracy and consistency of data. The function of integrity is
to make sure that the data is reliable and is not changed by unauthorized
persons.
·
Availability − The function of availability
in Network Security is to make sure that the data, network resources/services
are continuously available to the legitimate users, whenever they require it.
Passive Attacks
These attacks are not very
dangerous as they do not cause any modification to the data. These attacks are
generally done to secretly listen and monitor the communication of other
parties. Passive attacks are very difficult to detect because these attacks do
not change the information of the data.
There are two types of passive attacks in cryptography and network security:
Traffic analysis and Release of Message content
- Traffic Analysis: In this attack, an attacker tries to predict the
nature of communication by using information. The information such as
analyzing traffic, identify communication hosts, and frequency of
messages.
- Release of Message content: It is similar to hearing a telephone conversation
between two users. In this attack, the attacker can monitor the content of
the transmitted data such as email messages, etc.
Active attacks
These attacks involve some
modification of the data stream or the creation of a false stream. These
attacks can be classified in to four categories:
Masquerade – One entity
pretends to be a different entity.
Replay – involves
passive capture of a data unit and its subsequent transmission to produce an
unauthorized effect.
Modification of
messages –
Some portion of message is altered or the messages are delayed or
recorded, to produce an
unauthorized effect.
Denial of
service –
Prevents or inhibits the normal use or management of communication facilities.
Another form of service denial is the disruption of an entire network, either
by disabling the network or overloading it with messages so as to degrade
performance. It is quite difficult to prevent active attacks absolutely,
because to do so would require physical protection of all communication
facilities and paths at all times. Instead, the goal is to detect them and to
recover from any disruption or delays caused by them.
SECURITY ATTACKS
There are four general categories of attack which
are listed below.
Interruption
An asset of the system is destroyed or becomes
unavailable or unusable. This is an attack on availability e.g., destruction of
piece of hardware, cutting of a communication line or Disabling of file
management system.
Interception
An unauthorized party gains access to an asset. This
is an attack on confidentiality. Unauthorized party could be a person, a program
or a computer. e.g., wire tapping to capture data in the network, illicit
copying of files.
Modification
An unauthorized party not only gains access to but
tampers with an asset. This is an attack on integrity. e.g., changing values in
data file, altering a program, modifying the contents of messages being
transmitted in a network.
Fabrication
An unauthorized party inserts counterfeit objects
into the system. This is an attack on authenticity. e.g., insertion of spurious
message in a network or addition of records to a file.
Services and Mechanisms:
•
Confidentiality
•
Authentication
•
Integrity
•
Non-repudiation
•
Access
control
•
availability
Note: Interception causes loss of message confidentiality
Authentication:
Authentication is the process of recognizing a user’s identity. It is the
mechanism of associating an incoming request with a set of identifying
credentials.
Note: Fabrication is possible in absence of authentication
Integrity:
1.Prevent unauthorized users from making modifications to data or programs.
2. Prevent authorized users from making improper or unauthorized modifications.
3.Maintain internal and external consistency of data and programs.
Note: Modification causes loss of message integrity
Non
repudiation:
Non repudiation does not allow the sender of a
message to refute the claim of not sending that message.
•
Access
control specifies and controls who can access what
•
An access control mechanism controls which
clients or applications have access to
the server. Only properly authorized clients can connect to the server.
•
Two
different types of access control
mechanisms are used: user
based and host based.
Availability : means
that information is accessible to authorized users. It is basically an
assurance that your system and data are accessible by authorized users whenever
it's needed.
Security
mechanisms:
Symmetric and public key algorithms
Encryption/Decryption
methods fall into two categories.
Symmetric
key
Public
key
In
symmetric key algorithms, the encryption and decryption keys are known both to
sender
and
receiver. The encryption key is shared and the decryption key is easily
calculated from it.
In
many cases, the encryption and decryption keys are the same.
In
public key cryptography, encryption key is made public, but it is
computationally
infeasible to find the decryption key without the information known to the
receiver.
A MODEL FOR NETWORK SECURITY
A
message is to be transferred from one party to another across some sort of
internet. The two
parties,
who are the principals in this transaction, must cooperate for the exchange to
take place.
A
logical information channel is established by defining a route through the
internet from source
to
destination and by the cooperative use of communication protocols (e.g.,
TCP/IP) by the
two principals.
CONVENTIONAL ENCRYPTION
•
Referred conventional / private-key / single-key
• Sender and
recipient share a common key
Here the original message, referred to as plaintext, is converted into apparently random
nonsense,
referred to as cipher text. The encryption process consists of an algorithm and
a key.
The
key is a value independent of the plaintext. Changing the key changes the
output of the
algorithm.
Once the cipher text is produced, it may be transmitted. Upon reception, the
cipher
text can be transformed back to the original plaintext by using a decryption
algorithm
and
the same key that was used for encryption. The security depends on several
factors. First, the
encryption
algorithm must be powerful enough that it is impractical to decrypt a message
on
the
basis of cipher text alone. Beyond that, the security depends on the secrecy of
the key,
not
the secrecy of the algorithm.
•
Two requirements for secure use of
symmetric encryption:
–
A strong encryption algorithm
–
A secret key known only to sender / receiver
Y = EK(X)
X = DK(Y)
•
assume encryption algorithm is
known
• implies a secure channel to
distribute key
CLASSICAL ENCRYPTION TECHNIQUES
There
are two basic building blocks of all encryption techniques: substitution and
transposition.
SUBSTITUTION TECHNIQUES
A
substitution technique is one in which the letters of plaintext are replaced by
other letters or by
numbers
or symbols. If the plaintext is viewed as a sequence of bits, then substitution
involves replacing plaintext bit patterns with cipher text bit patterns.
Caesar cipher (or) shift cipher
The
earliest known use of a substitution cipher and the simplest was by Julius
Caesar. The Caesar cipher involves replacing each letter of the alphabet with
the letter standing 3 places
further
down the alphabet.
e.g.,
plain text : pay more money
Cipher
text: SDB PRUH PRQHB
Note
that the alphabet is wrapped around, so that letter following „z‟ is „a‟.
For
each plaintext letter p, substitute the cipher text letter c such that
C
= E(p) = (p+3) mod 26
A
shift may be any amount, so that general Caesar algorithm is
C
= E (p) = (p+k) mod 26
Where
k takes on a value in the range 1 to 25. The decryption algorithm is simply
P
= D(C) = (C-k) mod 26
Playfair cipher
The
best known multiple letter encryption cipher is the playfair, which treats
digrams
in
the plaintext as single units and translates these units into cipher text
digrams. The playfair
algorithm
is based on the use of 5x5 matrix of letters constructed using a keyword. Let
the
keyword be „monarchy‟. The matrix is constructed by filling in the letters of the keyword(minus duplicates) from left to right and from top to bottom, and then filling in the remainder ofthe matrix with the remaining letters in alphabetical order.The letter „i‟ and „j‟ count as one letter. Plaintext is encrypted two letters at a time
According
to the following rules:
Repeating
plaintext letters that would fall in the same pair are separated with a
Filler letter such as „x‟.Plaintext letters that fall in the same row of the matrix are each replaced by the letter to the
right,
with the first element of the row following the last.
Plaintext
letters that fall in the same column are replaced by the letter beneath, with
the top
element
of the column following the last.
Otherwise,
each plaintext letter is replaced by the letter that lies in its own row
And
the column occupied by the other plaintext letter.
Plaintext
= meet me at the school house
Splitting
two letters as a unit => me et me at th es ch o x ol ho us ex
Corresponding
cipher text => CL KL CL RS PD IL HY AV MP HF XL IU
Strength of playfair cipher
Playfair
cipher is a great advance over simple mono alphabetic ciphers.
Since
there are 26 letters, 26x26 = 676 diagrams are possible, so identification of
individual
diagram
is more difficult.
1.15.1.3 Polyalphabetic ciphers
M
O N A R
C
H Y B D
E
F G I/J K
L
P Q S T
U
V W X Z
Another way to improve on the simple monoalphabetic technique is to use different monoalphabetic substitutions as one proceeds through the plaintext message. The general name for this approach is polyalphabetic cipher. All the techniques have the following features in common.
A
set of related monoalphabetic substitution rules are used
A
key determines which particular rule is chosen for a given transformation.
Vigenere cipher
In
this scheme, the set of related monoalphabetic substitution rules consisting of
26 caesar ciphers with shifts of 0 through 25. Each cipher is denoted by a key letter. e.g., Caesar cipher with a shift of 3 is denoted by the key value 'd‟ (since a=0, b=1, c=2 and so on). To aid in understanding the scheme, a matrix known as vigenere tableau is Constructed
Each of the 26 ciphers is laid out horizontally, with the key letter for each cipher to its left. A normal alphabet for the plaintext runs across the top. The process of
Encryption is simple: Given a key letter X and a plaintext letter y, the cipher text is at theintersection of the row labeled x and the column labeled y; in this case, the ciphertext is V.
To encrypt a message, a key is needed that is as long as the message. Usually, the key is a repeating keyword.
e.g.,
key = d e c e p t i v e d e c e p t i v e d e c e p t i v e
PT
= w e a r e d i s c o v e r e d s av e y o u r s e l f
CT
= ZICVTWQNGRZGVTWAVZHCQYGLMGJ
Decryption is equally simple. The key letter again identifies the row. The position of the cipher text letter in that row determines the column, and the plaintext letter is at the top of that column.
Strength
of Vigenere cipher
o
There are multiple cipher text letters for each plaintext letter.
o
Letter frequency information is obscured.
One Time Pad Cipher
It is an unbreakable cryptosystem. It represents the message as a sequence of 0s and 1s. this can be accomplished by writing all numbers in binary, for example, or by using ASCII. The key is a random sequence of 0‟s and 1‟s of same length as the message. Once a key is used, it is discarded and never used again. The system can be expressed as
Follows:
Ci
= Pi Ki Ci - ith binary digit of cipher text Pi - ith binary digit of
plaintext
Ki - ith binary digit of key
Exclusive
OR operation
Thus
the cipher text is generated by performing the bitwise XOR of the plaintext and
the key.
Decryption
uses the same key. Because of the properties of XOR, decryption simply involves
the
same
bitwise operation:
Pi
= Ci Ki
e.g.,
plaintext = 0 0 1 0 1 0 0 1
Key
= 1 0 1 0 1 1 0 0
-------------------
ciphertext = 1 0 0 0 0 1 0 1
Advantage:
Encryption
method is completely unbreakable for a ciphertext only attack.
Disadvantages
It
requires a very long key which is expensive to produce and expensive to
transmit.
Once
a key is used, it is dangerous to reuse it for a second message; any knowledge
on
the first message would give knowledge of the second.
TRANSPOSITION TECHNIQUES
All
the techniques examined so far involve the substitution of a cipher text symbol
for
a plaintext symbol. A very different kind of mapping is achieved by performing
some sort of
permutation
on the plaintext letters. This technique is referred to as a transposition
cipher.
Rail
fence
is
simplest of such cipher, in which the plaintext is written down as a sequence
of diagonals and
then
read off as a sequence of rows.
Plaintext
= meet at the school house
To
encipher this message with a rail fence of depth 2, we write the message as
follows:
m
e a t e c o l o s
e
t t h s h o h u e
The
encrypted message is
MEATECOLOSETTHSHOHUE
Row Transposition Ciphers-
A
more complex scheme is to write the message in a rectangle, row by row, and
read the
message
off, column by column, but permute the order of the columns. The order of
columns then
becomes
the key of the algorithm.
e.g.,
plaintext = meet at the school house
Key
= 4 3 1 2 5 6 7
PT
= m e e t a t t
h
e s c h o o
l
h o u s e
CT
= ESOTCUEEHMHLAHSTOETO
A pure transposition cipher is easily recognized because it has the same letter frequencies as the original plaintext. The transposition cipher can be made significantly more secure by performing more than one stage of transposition. The result is more complex permutation that is not easily reconstructed.
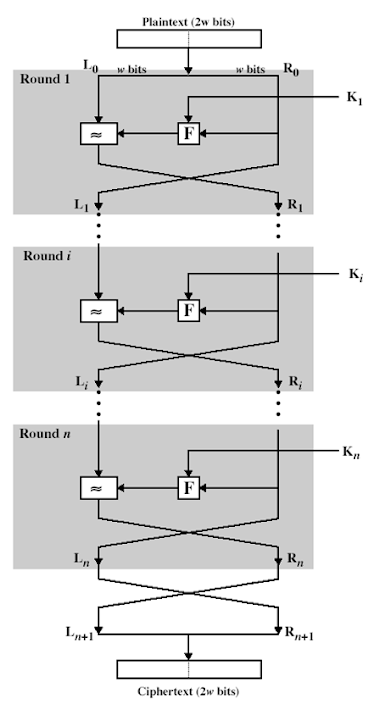
Feistel cipher structure
The
input to the encryption algorithm are a plaintext block of length 2w bits and a
key K.
the plaintext block is divided into two halves L0 and R0. The two halves of the data pass through „n‟ rounds of processing and then combine to produce the ciphertext block. Each round „i‟ has inputs Li-1 and Ri-1, derived from the previous round, as well as the subkey Ki, derived from the overall key K. in general, the subkeys Ki are different from K and from each other.
All rounds have the same structure. A substitution is performed on the left half of the data (as similar to S-DES). This is done by applying a round function F to the right half of the data and then taking the XOR of the output of that function and the left half of the data. The round function has the same general structure for each round but is parameterized by the round sub key ki. Following this substitution, a permutation is performed that consists of the interchange of the
two
halves of the data. This structure is a particular form of the
substitution-permutation network.
The
exact realization of a Feistel network depends on the choice of the following
parameters and
design
features:
Block size -
Increasing size improves security, but slows cipher
Key size -
Increasing size improves security, makes exhaustive key searching harder, but
may
slow
cipher
Number of rounds -
Increasing number improves security, but slows cipher
Subkey generation -
Greater complexity can make analysis harder, but slows cipher
Round function -
Greater complexity can make analysis harder, but slows cipher
Fast software en/decryption & ease of analysis - are more recent concerns for practical use and testing.
Fig: Classical Feistel Network
Fig: Feistel encryption and decryption
The
process of decryption is essentially the same as the encryption process. The
rule is as follows:
use the cipher text as input to the algorithm, but use the subkey ki in reverse order. i.e., kn in the first round, kn-1 in second round and so on. For clarity, we use the notation LEi and REi for data traveling through the decryption algorithm. The diagram below indicates that, at each round, the intermediate value of the decryption process is same (equal) to the corresponding value of the encryption process with two halves of the value swapped.
i.e.,
REi || LEi (or) equivalently RD16-i || LD16-i
After
the last iteration of the encryption process, the two halves of the output are
swapped, so that the cipher text is RE16 || LE16. The output of that round is the cipher text. Now take the cipher text and use it as input to the same algorithm. The input to the first round is RE16 || LE16, which is equal to the 32-bit swap of the output of the sixteenth round of the encryption process.
Now we will see how the output of the first round of the decryption process is equal to a32-bit swap of the input to the sixteenth round of the encryption process. First consider the encryption process,
LE16
= RE15
RE16
= LE15 F (RE15, K16) On the decryption side,
LD1
=RD0 = LE16 =RE15
RD1
= LD0 F (RD0, K16)
=
RE16 F (RE15, K16)
=
[LE15 F (RE15, K16)] F (RE15, K16)
=
LE15
Therefore,
LD1 = RE15
RD1
= LE15 In general, for the ith iteration of the encryption algorithm, LEi =
REi-1
REi
= LEi-1 F (REi-1, Ki)
Finally, the output
of the l
BLOCK CIPHER PRINCIPLES
Virtually,
all symmetric block encryption algorithms in current use are based on a
structure
referred
to as Fiestel block cipher. For that reason, it is important to examine the
design principles
of
the Fiestel cipher. We begin with a comparison
of stream cipher with block cipher.
•
A stream cipher is one that encrypts a digital data stream one bit or one byte
at a time. E.g,
vigenere
cipher. A block cipher is one in which a block of plaintext is treated as a whole and
used
to produce a cipher text block of equal length. Typically a block size of 64 or
128 bits is
used.
Block cipher principles
•
most symmetric block ciphers are based on a Feistel
Cipher Structure needed since must be
able
to decrypt ciphertext to recover messages efficiently. block ciphers look
like an extremely
large
substitution
•
would need table of 264 entries for a 64-bit block
•
Instead create from smaller building blocks
•
using idea of a product cipher in 1949 Claude Shannon introduced idea of
substitution-
permutation
(S-P) networks called modern substitution-transposition product cipher
these
form the basis of modern block ciphers
•
S-P networks are based on the two primitive cryptographic operations we have
seen before:
•
substitution (S-box)
•
permutation (P-box)
•
provide confusion and diffusion of message
•
diffusion – dissipates statistical structure of plaintext over bulk of
ciphertext
• confusion – makes relationship between ciphertext and
key as complex as possible
A=0,B=1,C=2,D=3,E=4,F=5,G=6,H=7,I=8,J=9,K=10,L=11,M=12,N=13,O=14,P=15,Q=16,R=17,S=18,T=19,U=20,V=21,W=22,X=23,Y=24,Z=25
A)What
is(A+N) MOD26 In this System0+13=13=N
B)What
is(C-10) MOD26 in this System
2-10=-8+26=18=S
C)What
is(W+Q) MOD26 in this System
=
22+16=38%26=12=M
Find
the particular and the general solutions to the following linear Diophantine equation
19x +13y = 20.
Gcd(19,13)=1
ax + by = c.
Particular
solution: x0 = (c/d)s and
y0 = (c/d)t
General
solutions: x = x0 + k (b/d) and
y = y0 − k(a/d)
34/22=>34=1*22+12
R1=q*R2+r
s=s1-qs2 t=t1-qt2
|
R1 |
R2 |
r |
S1 |
S2 |
s |
T1 |
T2 |
t |
q |
|
19 |
13 |
6 |
1 |
0 |
1 |
0 |
1 |
-1 |
1 |
|
13 |
6 |
1 |
0 |
1 |
0-2*1=-2 |
1 |
-1 |
1-2(-1)=3 |
2 |
|
6 |
1 |
0 |
1 |
-2 |
1-6*-2=13 |
-1 |
3 |
-1-6*3=-19 |
6 |
|
1 |
0 |
|
-2 |
13 |
|
3 |
-19 |
|
|
Gcd(19,13)=1
S=-2
T=3
Particular solution:
x0 = (c/d)s and y0
= (c/d)t
General
solutions: x = x0 + k (b/d) and
y = y0 − k(a/d)
X0=(20/1)*
-2=-40
Y0=(20/1)*3=60
X0=-40
Y0=60
X=-40+13K
Y=60-19K
Find the particular and the
general solutions to the following linear Diophantine equation 25x +10y = 15.




















No comments:
Post a Comment